In this Section, a set of geometrical applications derived from previous theoretical discussion are deeply investigated.

Computation of volume measure covered by intersecting geometrical loci

The first application studied enables the computation of the volume of the union of different loci. The whole mathematical process is deeply described hereby and it is concluded with the equivalent interpretation in terms of HSFGs.

Consider a finite set of geometrical loci, described with

where (mathbf{x }) is the generic coordinate in the space ({mathbb {R}}^D) in which the loci are embedded and (mathbf{q }_n) is a point in the the vector space of parameters which specifies the locus. Addressing the point (mathbf{q }_n) with index n is equal to consider such a point and its dimensionality to be independent from all the others. It is also assumed that (f_n) identifies a closed and compact volume

The aim is to find an expression which describes the volume that is effectively encompassed by the set of loci, namely

Clearly, the major difficulty stands in the fact that the sum of the measures

counts the intersections among different (V_n) a certain number of times, which will be later studied. Obviously, in the trivial case in which no intersections are present

Otherwise, in order to obtain (mu big (Vbig )) from (mu _S), each intersecting region has to be subtracted in an appropriate way. In other words, intersections have to be counted just once. For instance, consider a D = 2 scenario in which three squares ({mathcal {S}}_i), i : 1..3 intersect in region ({mathcal {R}}_i), i : 1..3 as shown in Fig. 2. Assuming v as the measure of the unit square, (mu _S) is equal to 48v, while (mu big ( V big )) = 30v. Defining ({mathcal {R}}_{1} = {mathcal {S}}_1cap {mathcal {S}}_2), ({mathcal {R}}_{2} = {mathcal {S}}_2cap {mathcal {S}}_3) and ({mathcal {R}}_3 = {mathcal {S}}_1cap {mathcal {S}}_2cap {mathcal {S}}_3), it results (in v units) that

As previously stated, the measure of each intersection region has to be subtracted a certain number of times that is equal to their multiplicity (kappa). But first, the characteristic function of the n-th volume has to be introduced:

According to the definition of the Heaviside used in this formula, the points verifying (f_n = 0) count as (vartheta _0) that is usually equal to 1 or 1/2, but they also may be not counted at all if (vartheta _0) is 0 or NaN. Then, the multiplicity of a point (mathbf{x }) is defined as follows:

In particular, the multiplicity of a point (mathbf{x }^*) which belongs just to one volume is (kappa (mathbf{x }^*)=0)

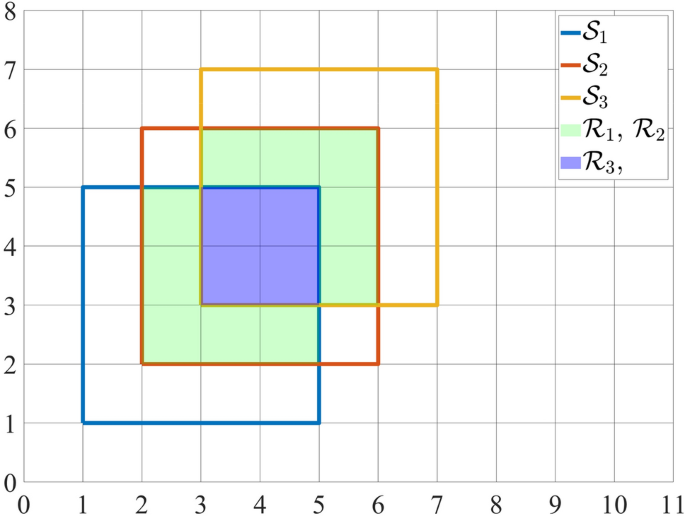
Example scenario of intersecting squares.

.

Consider a subspace ({mathcal {M}} subseteq {mathbb {R}}^D ni ‘ V_n subseteq {mathcal {M}} forall n). Analytically, the contribution that has to be subtracted from (28) is

However, an issue emerges in this formulation since

In fact, each point of ({mathcal {M}}) that does not belong to any (V_n) has -1 multiplicity, thus incorrectly increasing (mu _S). A third addendum which rectifies this behaviour is needed:

As a matter of fact, the integrand is equal to (1 forall mathbf{x } ni ‘ f_n > 0 forall n). The parameter (xi) is a shift that imposes the aforementioned behaviour. Indeed, points which do not belong to any volume return a value which is different from 0 according to the adopted definition of Heaviside:

Basically, as the results in (28)(33)(34) are brought together:

The expression above can be rewritten in a more compact manner. It is worth noting that (33) is equivalent to

The exchange between the sum and integral signs can be always done if N is finite, and also for (N rightarrow infty) under the hypothesis of Fubini’s Theorem. Moreover, the first integrand is equal to 1 for every point belonging to (V_n) at fixed n and it is 0 elsewhere. Therefore, the whole first addendum is equivalent to (28). Hence, (36) becomes:

Recalling results achieved in “HSF Boolean logic”, it is clear that (38) is the following HSFGs composition:

which does not correspond to any element of the (Psi _H) basis. However, it can be described by Algorithm 1 thanks to Theorem 4. Finally, this leads to:

which perfectly describes (27). This expression, as stated in Corollary 2, is also equivalent to

Remark 2

The characteristic function may not be defined on the locus (f_n=0) due to the definition of (vartheta _0). Nonetheless, the measure of a volume does not depend on the value assumed by (vartheta _0) because such value concerns the border which is a zero measure set.

Remark 3

It is worth noting that is sufficient to change the sign of the argument of all HSFs in Eq. (41) to characterize the dual formula for the computation of the intersection among all volumes, that is:

Again, recalling Corollary 2, an equivalent expression is

that well describes (43).

Error analysis

The error which is introduced by the use of the logistic function in place of Heaviside is addressed hereby. First, it is necessary to introduce the expression of the error:

Considering (18), introduce the variable (z=alpha sum _n(sigma _alpha +epsilon delta _alpha )(-f_n)-xi) and consider that any term (frac{d^k}{depsilon ^k}z), (kge 2) is zero, therefore it will not be written. As the same time, it can be reasonably assumed that the perturbation is zero at the border and, as a consequence, terms which are border-related are zero too.

Hence, it can be written:

Moreover, (frac{d^n}{dz^n}delta _alpha (z)=-frac{d^n}{dz^n}sigma _alpha (z)) because of the definition of (delta _alpha), so the first and third addenda for (kge 2) simplify at every term. Let (z’) be equal to (z(epsilon =0)=sum _nsigma _alpha (-f_n)-xi) and manipulate the following:

Finally, as (frac{d}{depsilon }z=alpha sum _ndelta (-f_n)) and the index of the Taylor series is moved back, it results that

Custom D-dimensional volumes

Another interesting application of Heaviside is the possibility to represent customizable volumes. In fact, the technique presented in previous Section is not limited just to analytical functions. Without loss of generality, consider (D = 2). Suppose that this desired area is defined by a closed polygonal chain of N segments, each of them lying on a given line described by (f_n) (or the vertical line (x = c), where c is a constant value). Clearly, (Theta (f_n)) is a binary representation of the inequality (f_n ge 0), because the equation (Theta (f_n) = 1) is satisfied only in a subspace of ({mathbb {R}}^2). Capitalizing the concept of AND HSFG described in “HSF Boolean logic”, the customizable area is cast with the following characteristic function:

This concept does not rely on choice of (f_n) as these can be anything, as long as ({mathcal {X}}_Theta = 1) encompasses a non-zero finite area. It is worth noting that with this formulation the Point-in-Polygon problem is inherently addressed by evaluating (50) in the desired location.

Remark 4

Reminding results of “Continuous HSF circuit definition”, also for this application is possible to define an equivalent SF form ({mathcal {X}}_sigma), taking advantage of (Lambda _sigma).

Remark 5

It should be noticed that

represents a general partition of input domain into a certain number of disjointed sub-domains of arbitrary shape.

Custom D-dimensional borders

According to the formulation proposed so far, a further important result is achieved when the objective is not to calculate the volume but to have an expression of its border. Once again, it is sufficient to exploit the AND HSFG. It is necessary that (vartheta _0 ne 0) to distinguish the locus of interest in the following manner:

where ({mathcal {Y}}_Theta) is the generic characteristic function which can be composed in one of the several ways previously discussed. In practise, when two face-to-face Heavisides are multiplied, the only geometrical locus that has non-zero value is the desired border. In other words, an equality constraint is imposed as will be seen in the next Section. In particular, if (vartheta _0 ne {0,1}) then it is just needed:

However, it must be noticed that if ({mathcal {Y}}_Theta) is composed of more than one function, and their borders intersect, then Eqs. (52) and (53) are not satisfied at the intersections of borders, except for Eq. (52) when (vartheta _0 = 1).

Another way to realize this locus is the substitution defined in (13) so that previous formulation is equivalent to:

where ({mathcal {Y}}_sigma) is the characteristic function expressed via SF. Still, intersections do not belong to (Gamma). If the limit is not taken, an interesting behaviour arises in the proximity of intersections due to the analyticity of (sigma):

For instance, consider the configuration in Fig. 3. It consists of a square centered in ([2 2]^T) and a circle in ([1 0]^T) which intersect in ([1 1]^T). Therefore, the ({mathcal {Y}}_sigma) in Eq. (55) is the sum of the characteristic functions of the square and the circle. The former is made with Eq. (50) and the usual substitution (13), while the latter is done with Eq. (31).
As (alpha ) increases, (Gamma _alpha) gets closer to the real intersection. The presence of the error owed to (alpha) results to be negligible, and even advantageous: the proposed formulation represents an optimum analytical approximation of the union border, which in principle (i.e. the exact border) should have no defined gradient at the intersection points.

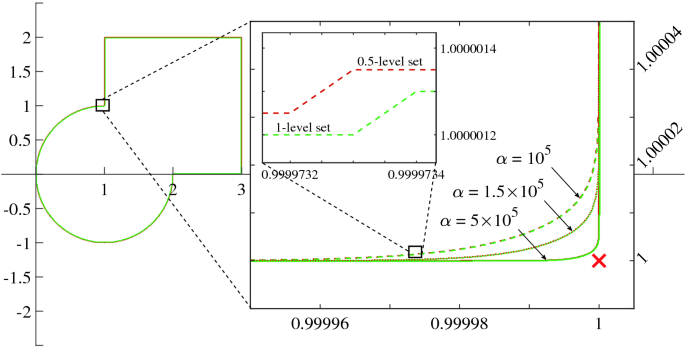
A custom border as function of (alpha).